問題:xが1に下から近付くとき x-x^2+x^4-x^8+x^{16}-x^{32}+…は収束するか?
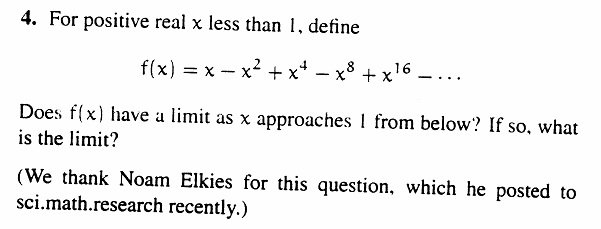
#数楽 添付画像の問題は https://www.uam.es/personal_pdi/ciencias/dragan/respub/Duren_Tauberian_Talk_2013-10_UAM.pdf … からの孫引き。Hardyさんが解決したらしい。私自身は自力で解けそうもないと思ったので答えをすぐに見た。コンピューターで数値計算すると楽しめると思います。pic.twitter.com/1jyzPl05zA
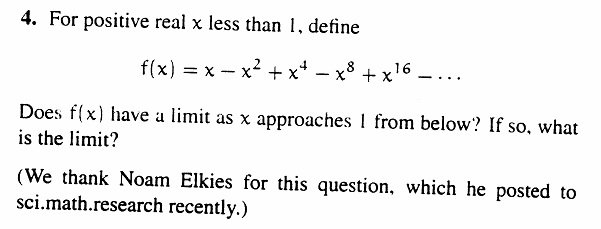
#数楽 一つ前のツイートで紹介した問題の邦訳:1未満の正の実数xに対してf(x)=x-x^2+x^4-x^8+x^16-…と定める。xが下から1に近付くときf(x)は収束するか?もしも収束するならその極限の値は何か?pic.twitter.com/1jyzPl05zA
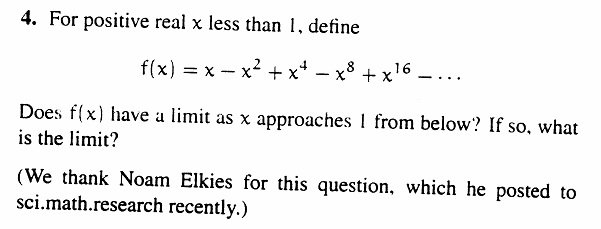
#数楽 この問題については数値計算すると非常に楽しそうです。答えは二つ前のツイートのリンク先のPDFファイルにあります。pic.twitter.com/1jyzPl05zA

#数楽 上の問題を動機付けに用いて、添付画像の定理のKaramataさんによるStone-Weierstrassの多項式近似定理を使った鮮やかな証明を紹介することは極めて教育的だと思いました。pic.twitter.com/gNKuMTENd1
#数楽 Wallisの公式のTauber型定理を用いた証明補題1: a_nが正値単調減少数列でΣ_{k=0}^n a_k〜an^α (n→∞)ならばa_n〜aαn^{α-1} (n→∞).これの積分版の証明は易しい。和分版は積分版に帰着。続く
#数楽 以上の2つの補題より、a_nが正値単調減少数列で、Σ_{n=1}^∞ a_n x^n〜1/(1-x)^α (x↑1)ならば、a_n〜n^{α-1}/Γ(α) (n→∞)となることがわかる。続く
#数楽 その結果を Σ_{n=1}^∞ a_n x^n=1/(1-x)^α、α=1/2 に適用するとWallisの公式a_n=2^{-2n} binom(2n,n)〜n^{α-1}/Γ(α)=1/√(πn) (n→∞)が得られる。
#数楽 以上で使った2つの補題はTauber型定理と呼ばれており、結構よく使われる。それらの結果を知っていれば、Wallisの公式は、(1-x)^{-1/2}のTaylor展開の係数に知っている結果を適用するだけでただちに得られる。
#数楽 その証明では、√πはΓ(1/2)の形で出て来る。Γ函数は、Karamataの方法をLaplace変換に適用する過程で、1/c^α=(1/Γ(α))∫_0^∞ e^{-ct} t^{α-1}dt を使うので出て来る。
#数楽 (1-x)^{-1/2}のべき級数展開の係数a_nはギャンブル(ランダムウォーク)での逆正弦法則を証明するときに出て来る。2n回の丁半博打で浮いていた時間が2kである確率はa_{2k}a_{2n-2k}に等しいことを示せる(結構面倒)。これに〜続く
#数楽 続き〜、これにWallisの公式a_n〜1/√(πn)を適用すれば、ギャンブルで浮いている時間の割合の確率分布が逆正弦分布にしたがうことを証明できる。その証明だとどうして逆正弦法則が成立するかは直観的にはよくわからない。
#数楽 以上は確率1/2で左右のどちらかに1ステップ移動するタイプの逆正弦法則の証明の仕方の概略。左右への移動の仕方を一般化した場合にはWallisの公式を使う部分をTauber型定理に置き換えれば同じようにして逆正弦法則を証明できる。
#数楽 そういうより一般のランダムウォークの場合の逆正弦法則の証明を読みたい人はF.Spitzer, Principles of Random Walk, GTM34(1976)の§20を見てください。
#数楽 Wallisの公式の話に戻るが、√πは大抵の場合Γ(1/2)の形で出て来る。というか、私の乏しい知識の範囲内では本質的にΓ(1/2)以外の形で自然に√πが出て来る例を知らない。
#数楽 初等的にも示せるWallisの公式をTauber型定理から出す証明を紹介したのは、一般的なランダムウォークで逆正弦法則を証明するときにまさにそういう形でKaramaraのTauber型定理を使うことを知ったから。
#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-05-01 … → http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf … 例の奴のVer.0.15(57頁)。簡単なTauber型定理とそのWallisの公式とx-x^2+x^4-x^8+x^{16}-…のx→1での漸近挙動への応用の解説を追加。
#数楽 http://www.math.harvard.edu/library/sternberg/ … のbook.pdfとLecture 8にも1次元単純ランダムウォークの場合のarc sine lawの詳しい証明が書いてありますね。
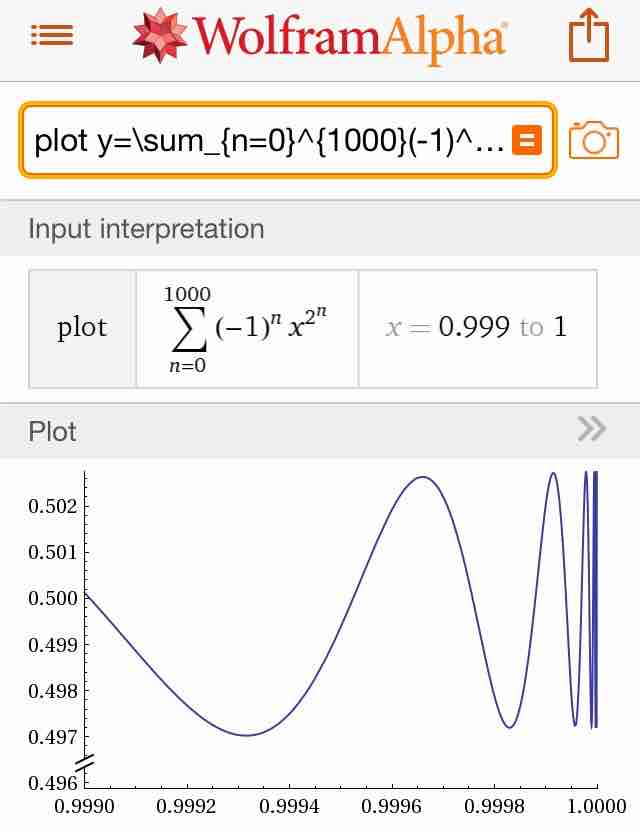
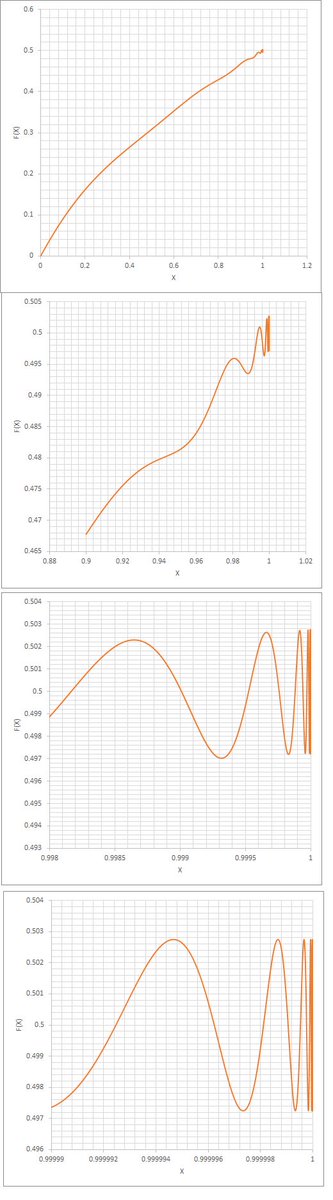
#数楽 WolframAlphaで x-x^2+x^4-x^8+x^{16}-…の0.999<x<1のでのグラフを書いてみた。確かに無限に振動しているっぽいよね(実際している)。pic.twitter.com/ESzdYarf17
#数楽 再掲 https://www.uam.es/personal_pdi/ciencias/dragan/respub/Duren_Tauberian_Talk_2013-10_UAM.pdf … ←これに x-x^2+x^4-x^8+x^{16}-…のx↑1での漸近挙動に関する詳しい解説があります。収束しないことはTauber型定理からすぐにわかる。
#数楽 例の奴のVer.0.16(61頁)。簡単なTauber型定理の証明が雑すぎたのでまじめに書き直した。書き直した直後なのでバグがたくさん残っているかも。 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-05-01 … → http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf …
#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-05-01 … → http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf … 例の内容ができるだけ雑多になるような方針で編集している学生向け解説ノートのVer.0.17(61頁)。やはりたくさんの誤りが残っていた。目についたものだけを訂正。
#数楽https://archive.org/details/ordersofinfinity00harduoft …Orders of infinity, the 'Infinitärcalcül' of Paul Du Bois-Reymondby Hardy, G. H. (Godfrey Harold), 1910
#数学 ついさっき、"Hardy field"という用語があることを初めて知った(用語を知らなくても概念的には明らかなもの)。 https://en.wikipedia.org/wiki/Hardy_field …
#数学 なるほど。orders of infinityを定義するときに無限振動の問題をどうするのかと思ったのだが、無限遠近傍で0函数でなければ決して0にならないという条件と微分で閉じているという条件で無限振動を排除しているのか。
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …



